6581. Attacking rooks

Chess inspired problems are a common source of exercises in algorithms classes. Starting with the well-known 8 - queens problem, several generalizations and variations were made. One of them is the n-rooks problem, which consists of placing n rooks in an n by n chessboard in such a way that they do not attack each other.

Professor Anand presented the n-rooks problem to his students. Since rooks only attack each other when they share a row or column, they soon discovered that the problem can be easily solved by placing the rooks along a main diagonal of the board. So, the professor decided to complicate the problem by adding some pawns to the board. In a board with pawns, two rooks attack each other if and only if they share a row or column and there is no pawn placed between them. Besides, pawns occupy some squares, which gives an additional restriction on which squares the rooks may be placed on.

Given the size of the board and the location of the pawns, tell Professor Anand the maximum number of rooks that can be placed on empty squares such that no two of them attack each other.

Input. The first line contains an integer n (1 ≤ n ≤ 100) representing the number of rows and columns of the board. Each of the next n lines contains a string of n characters. In the i-th of these strings, the j-th character represents the square in the i-th row and j-th column of the board. The character is either “.” (dot) or the uppercase letter “X”, indicating respectively an empty square or a square containing a pawn.

Output. Output a line with an integer representing the maximum number of rooks that can be placed on the empty squares of the board without attacking each other.

Sample input	Sample output
5 X.... X.... ..X.. .X... ....X	7

SOLUTION

graphs – maximum matching

Algorithm analysis

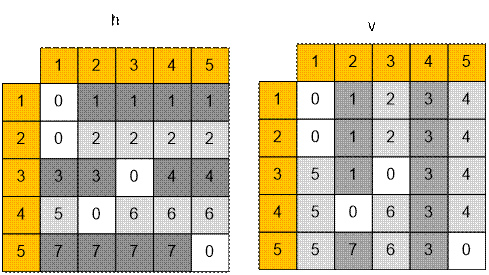
Let us construct matrices h of horizontal and v of vertical movement of rooks. The matrices contain zeros in the cells with pawns (symbols ‘X’).

The cells along which one rook can move in horizontal direction, conain identical numbers. Thus, we get a set of horizontal rectangles, each containing the same numbers in its cells. The same applies to the cells for vertical movements of a rook.

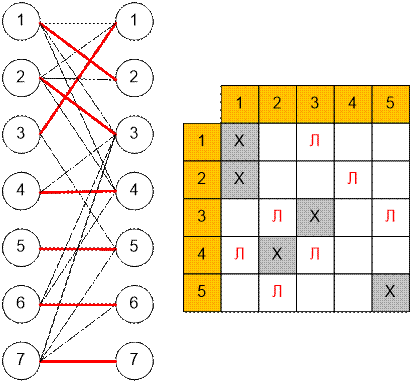
Next, we construct a bipartite graph. Each horizontal rectangle has some number i. Let’s assign it the vertex i of the left part of the graph. It should be connected to those vertices from the right part, which numbers coincide with the numbers of vertical rectangles crossing the i-th horizontal rectangle.

Now it remains to find the value of the maximum matching.

Example

Here is the matrices for horizontal and vertical movement of the rooks:

Next given the bipartite graph, the maximum matching and the optimal rook placement:

Algorithm realization

Declare the arrays.

#define MAX 111

char s[MAX][MAX];

int h[MAX][MAX], v[MAX][MAX];

vector<int> used, par, mt;

vector<int> g[MAX*MAX];

Start the depth first search from the vertex v. We try to find an augmenting path starting from v.

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

par[v] = to;

return 1;

}

}

return 0;

}

Find the maximum matching using the augmenting path algorithm.

void AugmentingPath(void)

{

mt.assign(ver, -1);

par.assign(hor, -1);

for (int run = 1; run; )

{

run = 0; used.assign(hor, 0);

for (int i = 1; i < hor; i++)

if ((par[i] == -1) && dfs(i)) run = 1;

}

}

The main part of the program. Read the input data.

cin >> n;

s[0] = string(n + 1, ' ');

for (i = 1; i <= n; i++)

{

cin >> s[i];

s[i] = " " + s[i];

}

Construct the matrices h and v, respectively, of the horizontal and vertical moves of the rooks on the board.

hor = ver = 1;

for(i = 1; i <= n; ++i)

for(j = 1; j <= n; ++j)

if(s[i][j] == '.')

{

h[i][j] = (s[i][j - 1] == '.' ? h[i][j - 1] : hor++);

v[i][j] = (s[i - 1][j] == '.' ? v[i - 1][j] : ver++);

Construct a bipartite graph.

g[h[i][j]].push_back(v[i][j]);

}

Start the search for the maximum matching.

AugmentingPath();

Compute the value of the maximum matching flow and print it.

flow = 0;

for (i = 1; i < ver; i++)

if (mt[i] != -1) flow++;

cout << flow;